ハンマー投げはどこで手を離せばいい？(遠心力、求心力とハンマー投げの科学)では、角運動する物体は接線方向に並進運動をしようとしているけど、中心に向かって引っ張ることで、円運動を続けていることを紹介しました。

 

一流選手ではハンマーの速度が30.0m/sにもなると言われています。

 

ここではその角運動における接線速度やその変化率の簡単な計算方法について説明していきます。

 

 

角運動する物体の並進速度(接線速度)の求め方

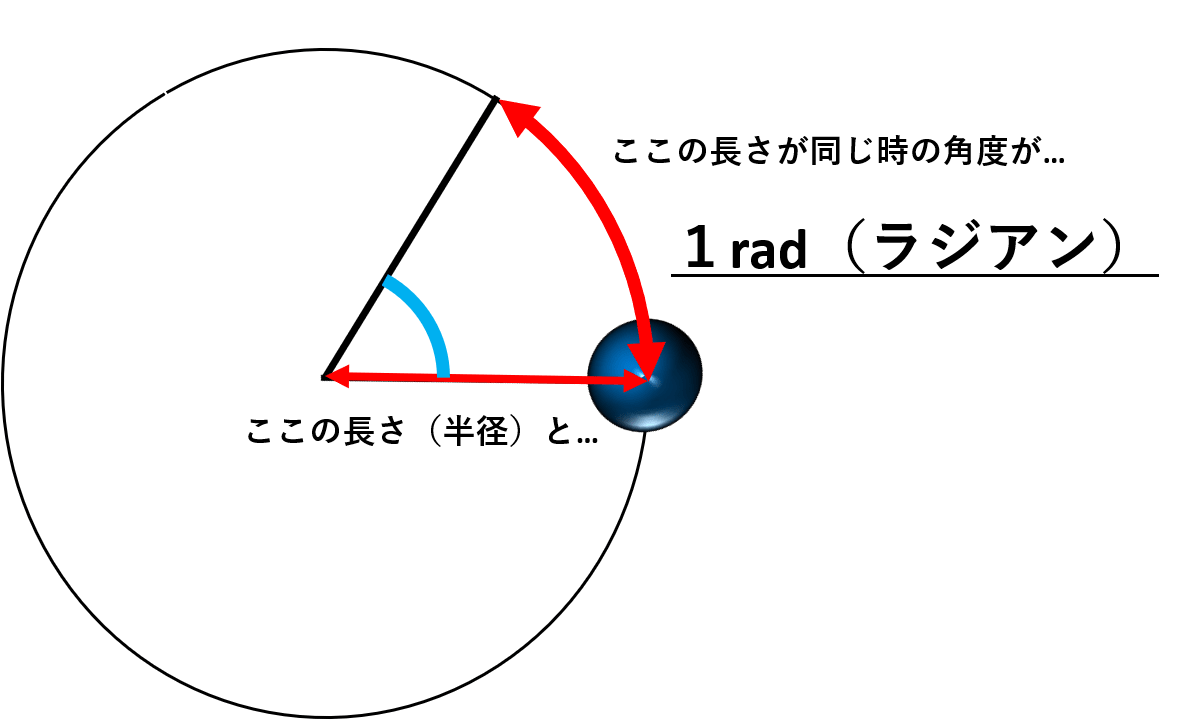
角度を表す単位として、rad(ラジアン)というものがあります。

 

これは端的に表すと、円の半径分の角度です。1radは下図の角度になります。

 

 

物理では、便宜上このradという単位で角度を記述することが多いのです。

 

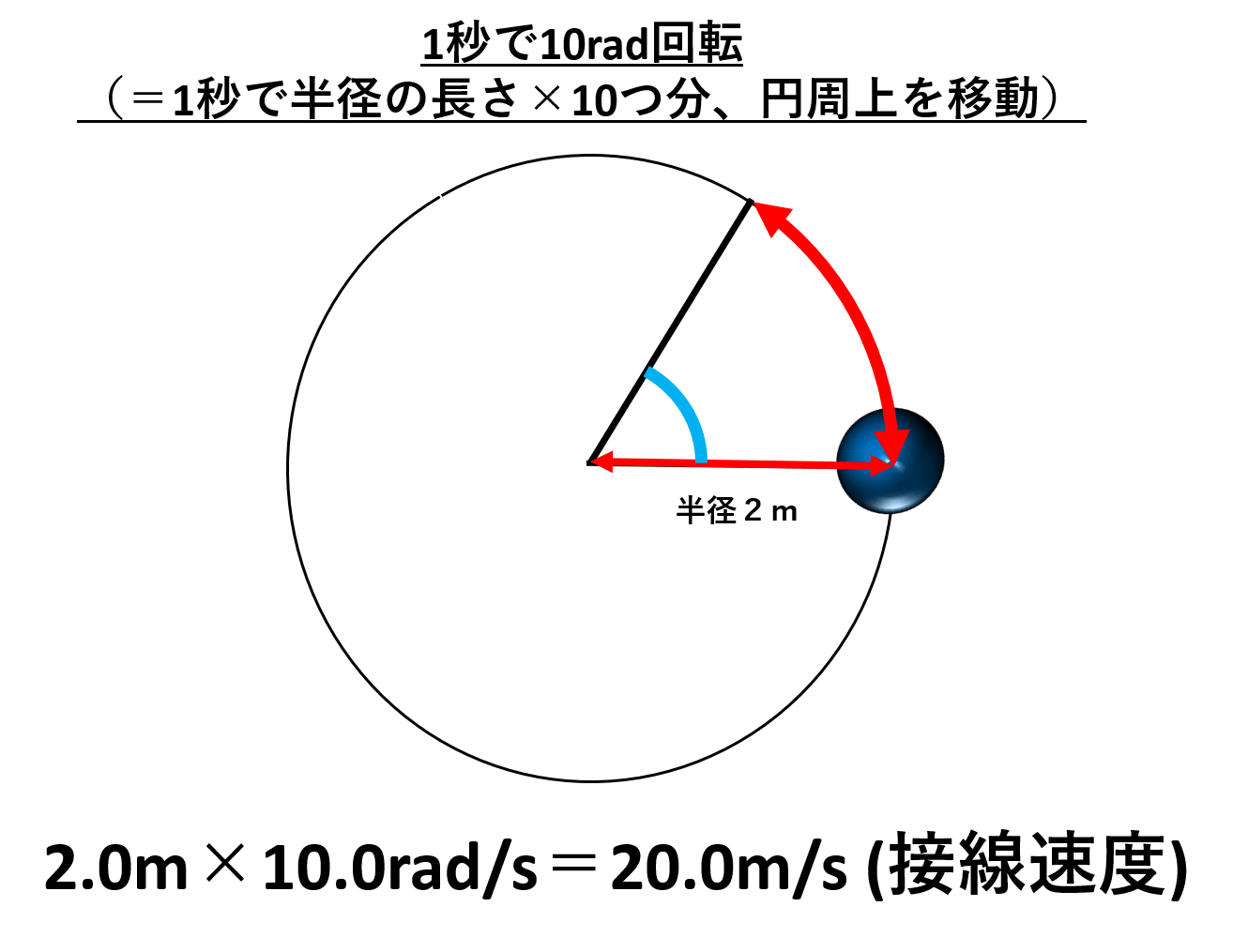
これを元に、円の半径が2mで、角速度が10.0rad/sで角運動する物体の接線速度を求めてみましょう。

 

10.0rad/sということは、1秒間に半径の10倍分の角度の変化があるということです。

 

なので、半径2m×10.0rad/s=20.0m/sとなり、この時の物体の並進速度は20.0m/sとなります。

 

 

このように、角運動する物体の並進速度(接線速度)は

 

 

で表すことができるわけです。

 

 

 

接線加速度の求め方

同様に、接線加速度も簡単に求めることができます。

 

接線加速度とは、接線方向に物体がどれだけ加速しようとしているかを表すものです。

 

例えば角加速度が2.0rad/s²で角運動していて、半径が2.0mの場合

 

角速度は半径2個分の長さ(の角度)ずつ上昇していくことになります。

 

したがって

 

2.0rad/s²×2.0m＝4.0m/s²

 

と、この時の角運動の接線方向の加速度が求まります。

 

 

 

求心加速度の求め方

角運動というのは、接線方向に移動したい物体を中心に引っ張ることで、円運動を保っているとも言えます。

 

中心に引っ張るということは、中心に向かって物体を加速させているということです。

 

引っ張ることで、中心に向かってどれくらいの加速度を生んでいるのかも、計算することができます。

 

この中心に向かう加速度のことを「求心加速度」といいます。これは以下の式で求めることができます。

 

 

なぜこの式になるのか、については以下のリンクを参照してください。

 

関連記事（わかりやすい高校物理の部屋）

・向心力：等速円運動の加速度

 

 

合わせて読みたい！