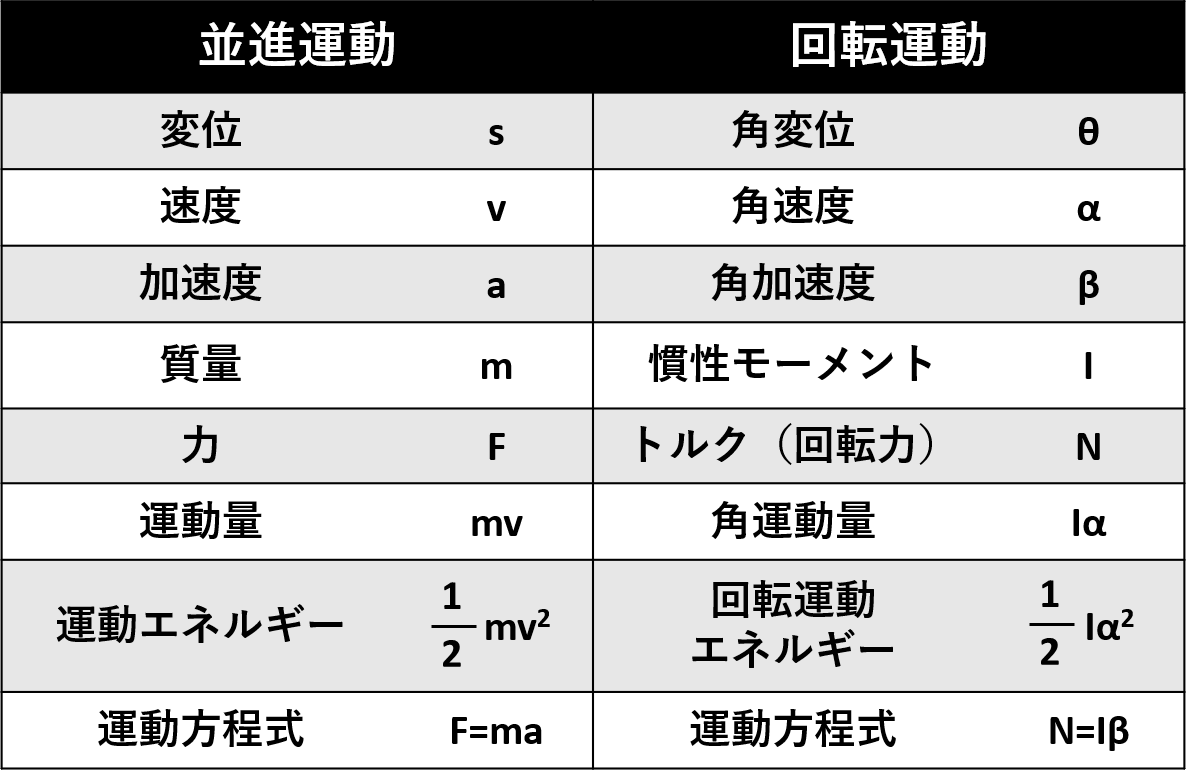
物体が回転せずに移動する「並進運動」では、ニュートンの運動方程式を用いて、力や物体の質量、加速度の関係を表すことができます。

 

関連記事

・「ニュートンの第2法則」運動方程式

 

そのニュートンの運動方程式は「F=ma」（力＝質量×加速度）で表され、大きな力を与えるほど、物体は加速し、質量が大きいほど、物体は加速しにくくなるわけです。

 

そして、ここで紹介するのが、この方程式の回転運動バージョンです。それが、オイラーの運動方程式です。

 

 

オイラーの運動方程式は

 

 

で表され、Nはトルク(回転力)、Iは慣性モーメント(物体の回しにくさ)、βは角加速度を示しています。

 

これは、基本的に並進の運動方程式と対応させて考えることができます。

 

F=maの力Fに当たるのが、回転力N。質量mに当たるのが、慣性モーメントI。加速度aに当たるのが、角加速度βというわけです。

 

また、並進運動の勢いを表す「運動量(mv)」、並進運動のエネルギーを表す「運動エネルギー(1/2mv²)」も同様に、回転運動の勢いを表す「角運動量(Ia)」、回転運動のエネルギーを表す「回転運動エネルギー(1/2Ia²)」と対比させることができます。

 

 

 

合わせて読みたい！